Attention

Transformer 的核心所在是自注意力机制，其允许模型在处理一个句子时，考虑句子中每个单词与其他所有单词的依赖关系，并使用这些信息来捕捉句子的内部结构和表示，最终计算单词之间的关联度（权重）。我们可以把自注意力机制分为三个阶段：

• 输入：从前文我们可以了解到，注意力机制接受查询（query）、键（key）和值（value）三个输入，但是对于自注意力来说，只有一个输入序列，Q、K、V都是来自于这个序列。这个输入序列是一个向量列表，且向量之间有一定的关系。以机器翻译为例，输入序列就是源语句或者目标语句，语句中每个token对应一个向量。
• 计算：自注意力机制会计算序列中每个向量与序列中其他向量的关系（也就是每个单词与句子中所有单词的关系），使得序列中的每个 token 都能感知其他 token。针对当前向量，自注意力机制会接受计算 Query（当前 token）与所有 Key（感兴趣的 token）的点积，应用 Softmax 函数在点积上以获取权重 Attention Weights，并使用权重对所有与之关联的 Value 进行加权平均。这样就可以把对其他单词的“理解”融入到当前处理的单词中。
• 输出：一个序列，比如一个向量列表，但是列表之中所有向量都考虑了其上下文关系，是蕴含了序列内部关系的全局特征表示。

具体如下图所示。

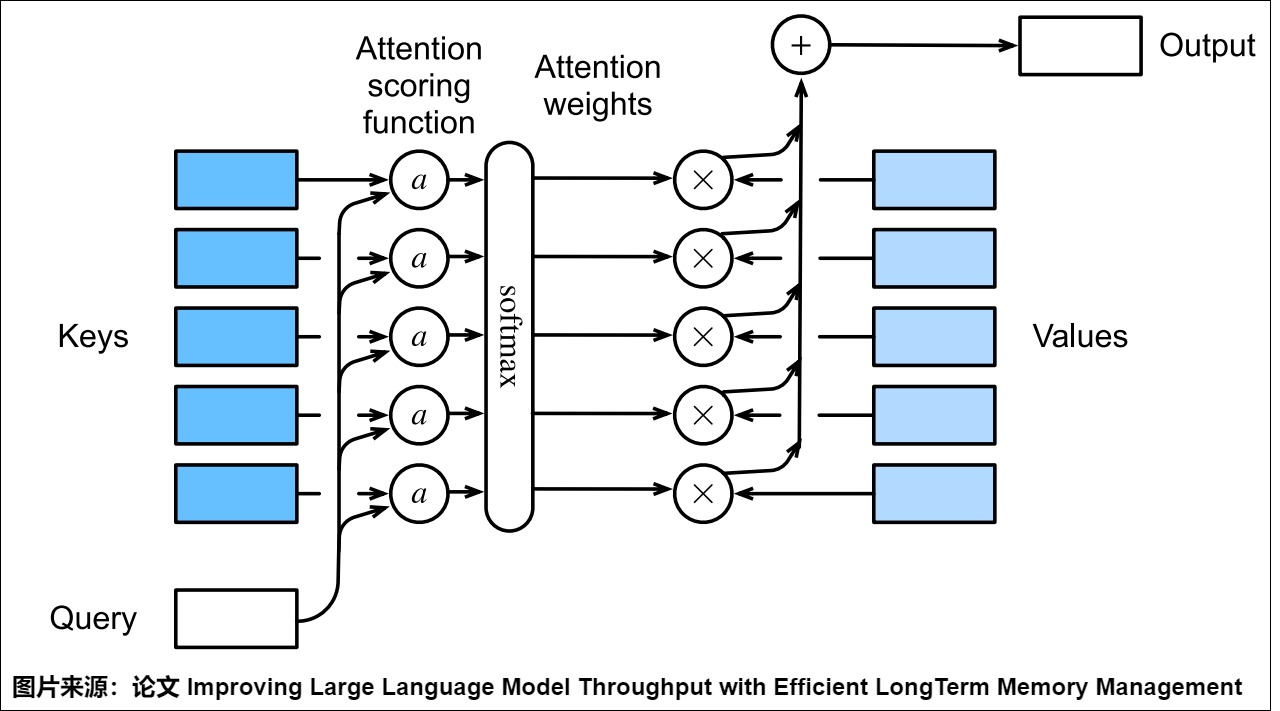
1.1 设计思路

自注意力并非Transformer首创，但之前在其他模型上效果不甚理想。所以我们好奇为什么Transformer依然使用自注意力呢，论文是这样解释其设计思路：

Motivating our use of self-attention we consider three desiderata. One is the total computational complexity per layer. Another is the amount of computation that can be parallelized, as measured by the minimum number of sequential operations required. The third is the path length between long-range dependencies in the network.

三个考虑因素我们具体解析如下。

• 每层的总计算复杂度。Transformer 的自注意力使用了 Scale Dot Product Attention Score 函数，相比于加性注意力减少了计算量，效果也是相似的。
• 并行计算。自注意力是可以并行化计算的，并行化计算量可以用所需的序列操作的最小数目来衡量。
• 网络中长距离依赖关系之间的路径长度。RNN捕捉词与词之间关系需要把句子从头看到尾，CNN需要层叠多个卷积层才能捕捉词与词之间关系，而自注意力是完全并行的，每个词可以直接关联。

虽然有若干优势，但是知易行难，Transformer如何做到？我们接下来一步一步进行分析。

1.2 输入

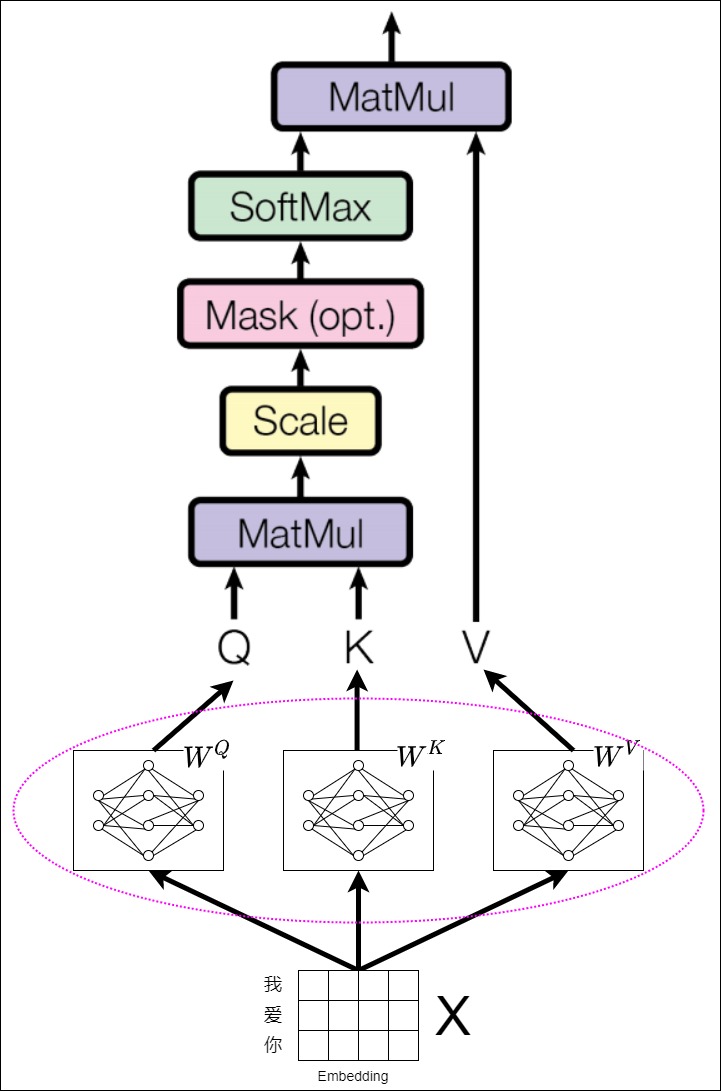
从宏观角度来说，Transformer只有一个输入序列，由这个序列派生出来Q、K和V。具体如下图所示。

从微观角度看，以编码器为例，自注意力的Q、K、V的来源有两种：

• 第一个编码器层的 QKV 由输向量 x 组成的矩阵 X 进行线性变化而来，线性变化就是用 $W^Q$, $W^K$, $W^V$ 进行矩阵乘法。
• 后续编码器层的 QKV 由上一个编码器层的输出经过线性变化而来。

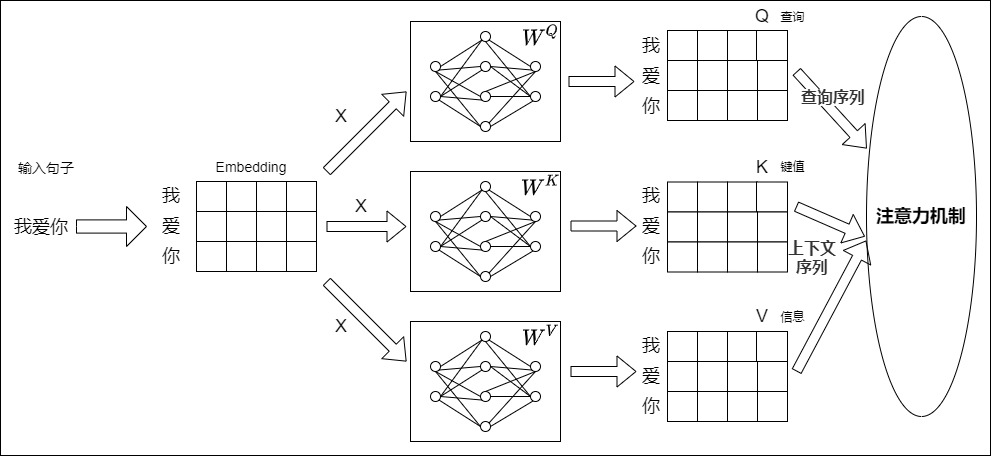
我们接下来以第一个编码器层为例，从源序列中的单个词开始来跟踪它们在 Transformer 中的路径。为了解释和可视化，我们暂时不用关心细节，只跟踪每个词对应的“行”。

假如我们进行英译中，输入中文：我爱你。假定模型维度为 d，输入序列长度为 L。源序列首先通过 Embedding 和 Position Embedding，该层为序列中的每个单词生成嵌入向量，这些嵌入向量构成的矩阵就是 $X$，shape 为 (L, d)

输入序列接下来会通过三个矩阵$\mathbf{W}^K \in \mathbb{R}^{d \times d_k}$，$\mathbf{W}^Q \in \mathbb{R}^{d \times d_q}$，$\mathbf{W}^V \in \mathbb{R}^{d \times d_v}$进行转换。具体来说，输入序列的每一个元素$x_i \in \mathbb{R}^d$会分别乘以这三个矩阵，得到

$$

\begin{align*}

q_i &= x_i \mathbf{W}^Q \

k_i &= x_i \mathbf{W}^K \

v_i &= x_i \mathbf{W}^V

\end{align*}

$$

把 $L$ 个 $q_i$ 堆叠起来就得到矩阵 $\mathbf{Q} \in \mathbb{R}^{L \times d_q}$，类似可以得到矩阵 $\mathbf{K} \in \mathbb{R}^{L \times d_k}$，$\mathbf{V} \in \mathbb{R}^{L \times d_v}$。或者直接用矩阵形式表达： $$

\begin{align*} \mathbf{Q} &= \mathbf{X}\mathbf{W}^Q \ \mathbf{K} &= \mathbf{X}\mathbf{W}^K \ \mathbf{V} &= \mathbf{X}\mathbf{W}^V \end{align*} $$ 这个三个独立的矩阵Q、K、V会被用来计算注意力得分。这些矩阵的每一行“都”是一个向量，对应于源序列中的一个词。每个这样的“行”都是通过一系列的诸如嵌入、位置编码和线性变换等转换，从其相应的源词中产生。而所有这些的转换都是可训练的操作。这意味着在这些操作中使用的权重不是预先确定的，而是利用反向传播机制进行学习得到的。

1.3 QKV解析

自注意力机制中第一步就是用 Token 来生成查询向量、键向量和值向量，也就是用到了 query，key，value（各种相关论文、网址之中也缩写为 q、k、v）这三个概念。Query 向量代表当前正在处理的 token 或位置，它表示模型需要“查询”的信息。Key 向量代表序列中每个 token 的唯一标识，用于与 Query 进行比较。Value 向量包含序列中每个 token 的实际内容或特征，它对生成当前 token 的输出有贡献。

要理解 LLM 的底层实现原理，就必须要了解 Transformers Block 里面的 QKV 矩阵，因为前沿的大模型研究工作很大一部分就是看 QKV 矩阵去做的，比如注意力、量化、低秩压缩等等，目标是在保证效果不变坏的前提下，进行对性能和存储的极致压缩。其本质原因是因为 QKV 权重占比着大语言模型50%以上的权重比例，在推理过程中，QKV 存储量还会随着上下文长度的增长而线性增长，计算量也平方增加。可以说，query，key，value 对于 Transformers 和自注意力机制至关重要。

相信大家一直都有个疑问，为什么要取 QKV 这些名字？这一套思想到底怎么去理解？之前篇幅中介绍过 QKV，但是始终没有深入，本篇会进行详细分析。因为深度学习其实是带有实践性质的科学，尚未找到确切的理论分析。所以接下来我们从不同理解的角度来阐释，希望读者能够从其中对 QKV 有所理解。

心理学角度

有研究人员发现，注意力机制可以追溯到美国心理学之父威廉·詹姆斯在19世纪90年代提出的非自主性提示（nonvolitional cue）、自主性提示（volitional cue）和感官输入（Sensory inputs）这几个概念。而这三个概念就分别可以对应到Key张量，Query张量和与Key有对应关系的Value张量，然后由这三者构建了注意力机制。

我们用个通俗例子来分析下。本来你去买盐（带有目的性的关注度，即自主性提示），结果你到了商店，发现了变形金刚，你注意力都被变形金刚（下意识的关注度，即非自主性提示）吸引了。我们可以得到：

• Key：一系列物品（盐和变形金刚）。
• Value：这一系列物品对人下意识的吸引力（在你下意识中，变形金刚的吸引力肯定比盐要高）。
• Query：你想要的物品（盐）。

注意力作用就是让盐（目标物品）所对应的权重值变高。这样使用该’权重向量’乘‘key’后，即使目标物品“下意识的吸引力（即key）”不够高，但是因为目标物品对应的权重高，其他物品对应的权重小，故选择到目标物品的可能性也会变大。

数据库角度

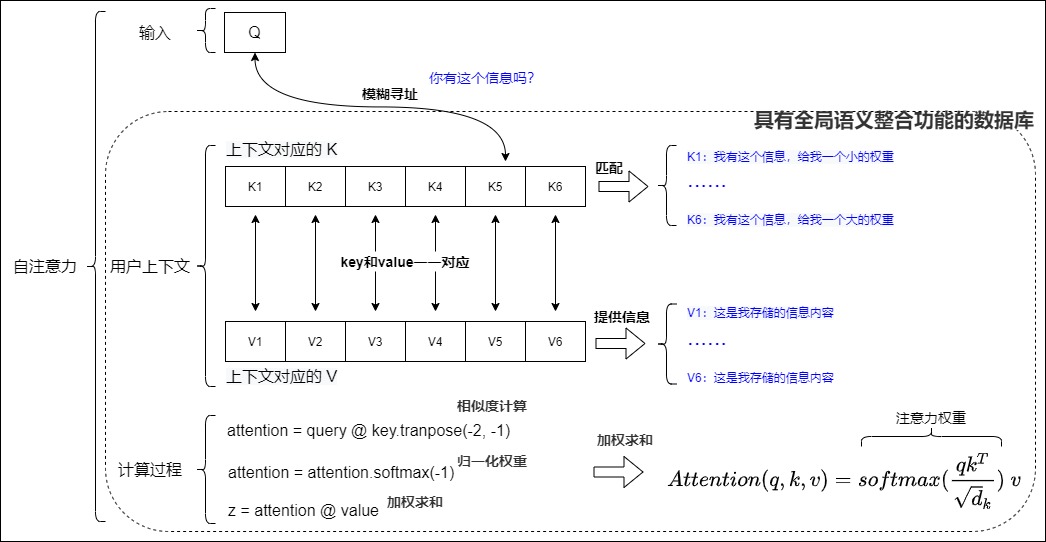
query，key，value 的名称也暗示了整个注意力计算的思路，因此我们从搜索领域的业务来看 Q、K、V 可能更好理解。我们把注意力机制看作是一种模糊寻址，或者说是一个模糊的、可微分的、向量化的数据库（或者字典）查找机制。Q、K、V 这三者的关系就是：找到与现有数据（Query）相似或者相关的数据（Key）所对应的内容（Value）。其具体特点如下：

• Key 和 Value 是数据库的组件。
• 数据库中每个元素由地址 Key 和值 Value 组成（一个 <Key,Value> 数据对）。或者说，Key 这个地址里面就存放了 Value。
• Key是地址，就是要查找的位置。该地址总结了地址中Value的特征，或者说Key可以体现Value上的语义信息。
• Value是与地址Key相关联的值，是表征语义的真实数据，是对外提供的使用者所需的内容。
• Query 是查询信息，是任务相关的变量。假设当前有个 Key=Query 的查询，该查询会通过 Query 和存储器内所有元素 Key 的地址进行相似性比较来寻址，其目的是取出数据库中对应的 Value 值。自注意力机制中这种 Q 和 K 一问一答的形式，问的就是 Q 和 K 两个词之间的紧密程度。直观地说，Key 是 Query（我们正在寻找什么）和 Value（我们将实际获得什么）之间的桥梁。
• 普通的字典查找是精确匹配，即依据匹配的键来返回其对应的值，而且只从存储内容里面找出一条内容。而注意力机制是向量化+模糊匹配+合并的组合使用。其会根据 Query 和 Key 的相似性来计算每个 Key 的相似度或者匹配程度（即注意力权重）。然后从每个 Key 地址都会取出 Value，并依据匹配程度对这些 value 做加权求和，这个相似度得分决定了相应 Value 在最终输出中的权重。

用通俗例子来讲解，假如我们在淘宝上进搜索”李宁鞋“，Query（Q）就是你在搜索栏输入的查询内容。Key（K）就是在页面上返回的商品描述、标题，其实就是数据库中与候选商品相关的关键字。Value（V）就是李宁商品本身。注意力机制就是这个查询过程，即注意力是把你要查询的Q与淘宝数据库中的K进行比较，计算出这些K与Q的相似度，最终返回相似度最高的若干商品V。流程如下：

1. 用 Query 与数据库内所有 Keys 进行计算相似度（查询的相关性，即你有多大概率是我要查的东西）。
2. 得到相似度之后，对结果进行排序。
3. 基于相似度排序结果，得到需要获取的商品 ID
4. 依据商品 ID 来获取对应的 Values。

   

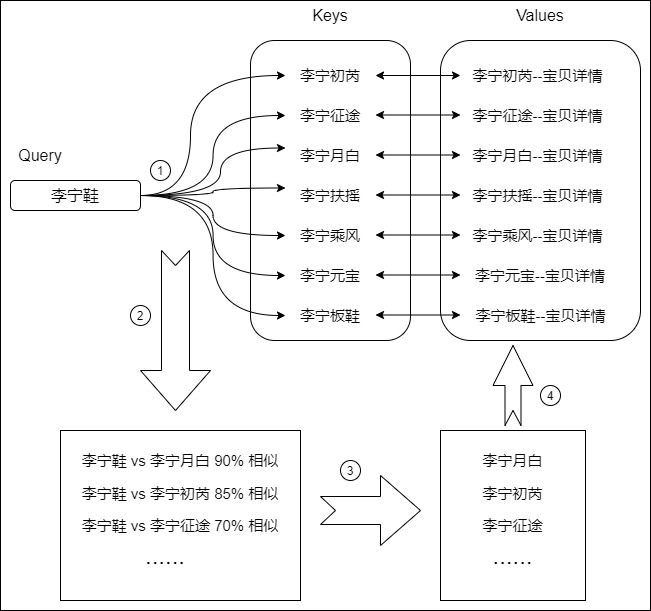
因此，自注意力机制中的QKV思想，本质是一个具有全局语义整合功能的数据库。<Key,Value>数据对就是数据库的元素，Q就是任务相关的查询向量。

下图从数据库角度展示了自注意力的细节。

seq2seq角度

让我们回到具体任务上来分析，可能会更加清晰一点。比如在机器翻译任务中，query 可以定义成解码器中某一步的隐状态，即对上一个词的预测输出。key 是编码器中每个时间步的隐状态，我们用每一个 query 对所有 key 都做一个对齐，于是解码器的每一步都会得到一个不一样的对齐向量。或者说，编码器的编码序列（Encoded sequence）提供 key 和 value 。Hidden state of Decoder 提供 query 。这就好比解码器要去编码器的编码序列那里查字典一样。

重构词向量角度

前面我们从数据库角度来看到如何寻址获取讯息，其最终目的是输出一个新向量。在新的向量中，每一个维度的数值都是由几个词向量在这一维度的数值加权求和得来的。因此，自注意力机制的核心是重构词向量（查询+聚合），每个输入单词的编码输出都会通过注意力机制引入其余单词的编码信息。

相互操作

人类在读一篇文章时，为了理解一句话的意思，你不仅会关注这句话本身，还会回看上下文中相关的其他句子或词语。我们还是以之前两个句子为例进行解释。

• Several distributor transformers had fallen from the poles, and secondary wires were down.
• Transformer models have emerged as the most widely used architecture in applications such as natural language processing and image classification.

如何才能对“Transformer”这个多义词进行语义区分？我们必须考虑单词的上下文才能更好的把单词的语义识别出来，即不仅仅要考虑到词本身，还要考虑其他词对这个词的影响，也就是语境的影响。比如第一个句子的“pole”、”fallen”和“wires”这几个邻近单词暗示了“Transformer”和物理环境相关。第二个句子的“model”和“natural language processing and image classification”则直接告诉我们此处的“Transformer”是深度学习相关概念。最终我们通过上下文语境（句子中的其他词）可以推断“Transformer”的准确含义。

原理我们知道，但是如何实践？如何通过句子中的其它词来推断？人类可以知道哪些词提供了上下文，但计算机却毫无头绪，因为计算机只处理数字。解决方案就是注意力机制在Transformer中所模拟的过程。

Transformer 通过点积这个提取特征的操作将输入序列中的每个词与其他词关联起来，也就是词之间进行互相操作。然后通过加权求和把这些词加起来，最终可以捕捉到某个特定的词和句子中其他每个词之间的一些互动。于是修改后的词如下：

• transformer 1 = 0.7 transformer + 0.1 pole + 0.1 fallen + 0.1 wires
• transformer 2 = 0.6 transformer + 0.1 language + 0.1 image + 0.2 model

最终两个transformer单词就通过和句子中其它单词的操作完成了对本身语义的重构。

我们接下来具体看看提取特征和加权求和这两个操作。

提取特征

K提取的特征是如何获得的呢？根据自注意力的思想和人脑的机制，我们需要先看过所有项才能准确地定义某一个项。因此，对于每一个查询语句Q，注意力机制会：

• 用这个 Query 和每 个 Key 通过内积的方式来计算出相似度或者相关性，以此来决定哪个元素会对目标元素造成多少影响（即 Key 和 Query 会得出对齐系数）。Key 与 Query 越相似或者说越相关，Value 的影响力就越大，越应该承担更多的对输入的预测。
• 然后注意力机制会对点积结果进行一个 softmax 操作，使得所有 value 的权重总和为1。这是为了保证所有源元素贡献的特征总量保持一定。如果有多个 key 都与 query 高度相似，那么它们各自的通道都会只打开一部分（好像“注意力分散在这几个源元素上”）。从这个角度来看，可以理解为输出是在 value 之间根据 key-query 的相似度进行内插值的结果。很明显，这个输出表征携带了其它单词的信息。
• 最后得到的矩阵 Y ，就是输入矩阵 X 融合了上下文信息得到的在隐空间的语义矩阵，每一行代表一个token。

如果是训练过程，则在拿到Y之后，模型会通过损失函数进行计算，最终经过反向传播后，Q就能逐渐学习到V的特征。这个机制让模型可以基于相同的注意力机制学习到不同的行为，并且能够捕获序列内各种范围的依赖关系。

加权求和

让我们通过一个真实例子来理解加权求和操作。

我们希望了解郁达夫（Query），但是因为人的精力有限，所以需要把有限的精力集中在重点信息上，这样可以用更少的资源快速获取最有用的信息，效果更好。图书馆（Source）里面有很多书（Value），我们看书就相当于获取其书中的详细信息（Value）。为了提升效率，我们给每本书做了编号和信息摘要（Key）。于是我们可以通过 Key 搜索出来很多书，比如《薄奠》，《沉沦》，《迟桂花》，《春风沉醉的晚上》，《归航》等等，也能搜出来《大众文艺》（郁达夫曾任主编）。

通过将 Query 与 Key 中携带的信息摘要相比较，我们可以知道它们的相关程度有多高。相关性越高的书，其权重越大。前面几本书的权重就高，需要分配更多的注意力来重点看，《大众文艺》的权重就显然要略低，大致浏览即可。

假如我们一共要花费11小时在了解郁达夫上。我们会分别花费2小时在《薄奠》，《沉沦》，《迟桂花》，《春风沉醉的晚上》，《归航》，花费1小时在《大众文艺》上。我们把时间归一化成和为1的概率值，得到 [0.18, 0.18, 0.18, 0.18, 0.18, 0.09]，所以郁达夫 = 0.18《薄奠》+ 0.18《沉沦》+ 0.18《迟桂花》+ 0.18《春风沉醉的晚上》+0.18《归航》+0.09《大众文艺》。最终得到的信息是所有书籍内容按照权重综合起来的结果。这样当我们全部看完以上几本书后，就对郁达夫有一个全面的了解，就是加权求和。

注意力机制本质就是使用 Q 和 K 来计算出“注意力权重“，然后利用注意力权重对Ｖ进行加权求和。从机制上看，注意力机制聚焦的过程体现在权重系数上，权重越大表示投射更多的注意力在对应的值上，即权重代表了信息的重要性。注意力机制可以被解释为将多个局部信息源路由到一个局部表征的全局树结构中。在这个例子中，我们计算相关性就相当于注意力机制中的 $QK^T$ ，归一化就是 softmax 操作，然后通过加权求和取得最后的阅读量/特征向量。

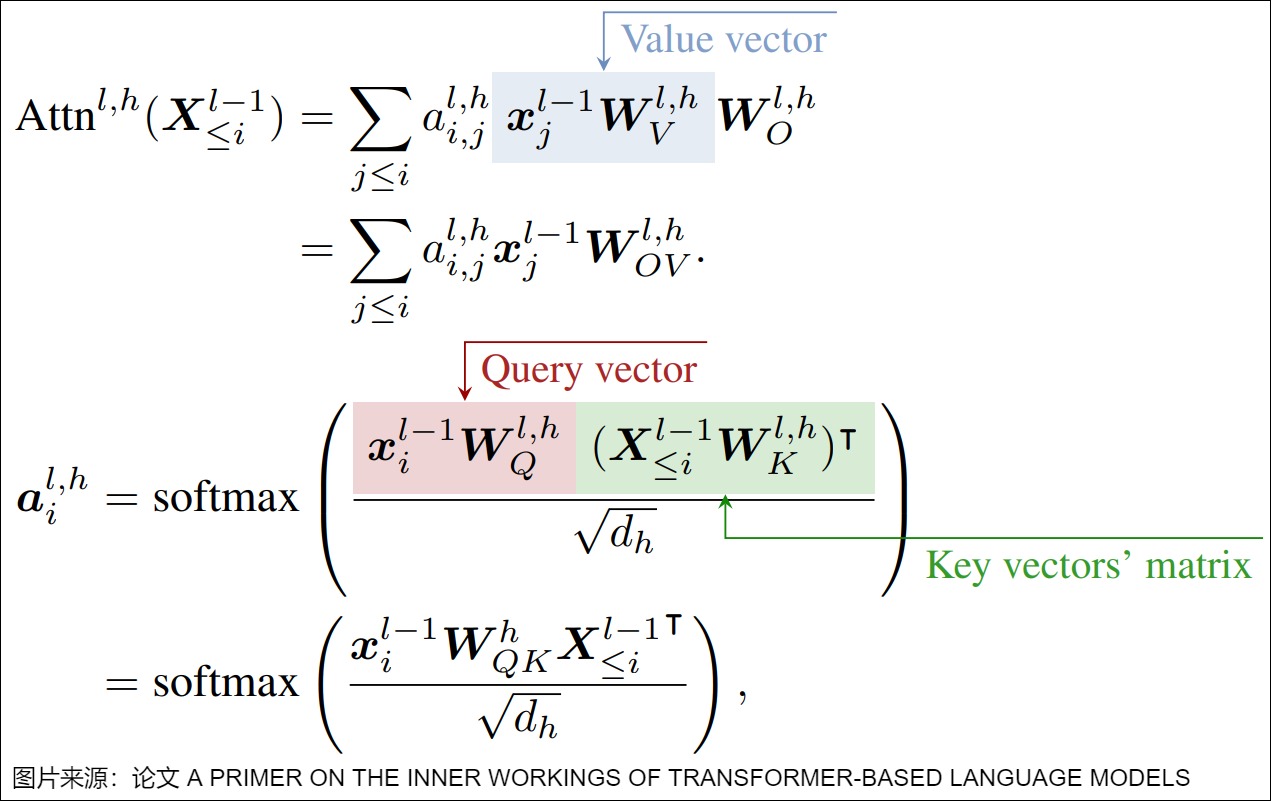
Elhage重构了注意力头的表达形式（仍然等价于vanilla Transformer的设计），重构的表示可以表达为如下公式，可以看出来相互操作、提取特征和加权求和的特点。

1.4 小结

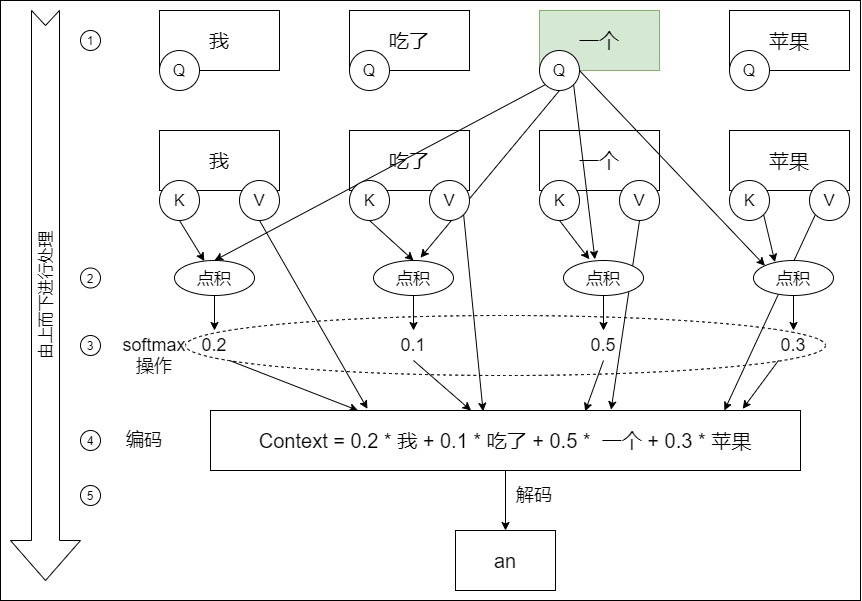
我们以”我吃了一个苹果“为例来看看自注意力的流程。

• 首先确定哪个目标 token 来作自注意力机制，这个目标 token 是”一个“，即让”一个“来判断它和其他三个词之间的关系
• ”一个“会对”我吃了一个苹果“这句话中所有token都做一遍点积，然后做softmax操作做归一化，生成权重。
• 用权重和V向量相乘，得到加权之后的向量，即”一个“可以用0.2 * 我 、0.1 * 吃了、 0.5 * 一个和 0.3 * 苹果 来组合表示。所以”一个“的带有词关联性的表示为：一个=0.2×我+0.1×吃了+0.5×一个+0.3×苹果。在新的向量中，每一个维度的数值都是由几个词向量在这一维度的数值加权求和得来的，这个新的向量就是"一个"词向量经过注意力机制加权求和之后的表示，该词具备词关联性。
• 解码输出”an“。

1

\text{Attention}(\text{Target}, \text{Source}) = \text{Attention}(\text{Query}, \text{Source}) = \sum_{i=1}^{\text{Length}_{\text{Source}}} \text{Similarity}(\text{Query}, \text{Key}_i) * \text{Value}_i

可以看出，“一个”在全句中，除了自己之外，与“苹果”关联度最大，其次是“我”。所以“一个”这个词也可以理解为“我-一个-苹果”。这便把“一个”在这句话中的本质通过“变形”给体现出来了。“一个”本身并没有变，而是通过“变形”展示出了另外一种变体状态“我-一个-苹果”。外在没变，灵魂变了。

可以看到，自注意力机制是一种动态的、数据驱动的变换，是对输入向量空间的一种动态变换。这种变换不是固定的，而是依赖于输入数据的内容来决定的。因此，注意力的本质思想可以改写为如下公式：通过计算相似性得出权重最后加权求和。

$$\text{Attention}(\text{Target}, \text{Source}) = \text{Attention}(\text{Query}, \text{Source}) = \sum_{i=1}^{\text{Length}_{\text{Source}}} \text{Similarity}(\text{Query}, \text{Key}_i) * \text{Value}_i$$

0x02 实现

2.1 权重矩阵

现在的神经网络很少有将 Word Embedding 直接参与一些网络结构的计算，一般都会先做一个线性变换。实际上，Transformer 是把每个 token 的 Embedding 向量 $x$ 分别乘以三个不同的权重矩阵 $W^K, W^Q, W^V$，作三次线性投影（或称为线性变换），派生出 Q、K、V 三个矩阵（注意，这里提到的“权重”，是指神经网络中的连接权重，与 Attention 中 token 之间的语义关联权重不是一个意思）。而且，每个 Transformer block 都有自己的 $W^K, W^Q, W^V$。

这三个权重矩阵是在模型训练过程中通过反向传播训练出来的。在训练阶段，模型会对这三个权重矩阵进行随机初始化。在模型的执行阶段（预测阶段），这三个矩阵是固定的，即 Transformer 神经网络架构中固定的节点连接权重，是早就被预先训练好的了（Pre-Trained）。$W^K, W^Q, W^V$ 这三个矩阵实际上是模型学会的分配 Q，K，V 的逻辑。

为什么要引入权重矩阵？或者说，为什么不直接使用 X 而要对其进行线性变换？为何要从一个序列中的每一个 token 的 Embedding 派生出三个向量 Q、K、V（即查询向量、键向量和值向量）呢？主要可以从如下方面进行思考。

首先看看直接使用Embedding的缺点。

• 输入的 Embedding 其实只做了一次线性变换，特征提取能力或者表示学习的能力及其有限。
• 一个点积操作中没有什么可以学的参数。为了识别不一样的模式，我们希望有不一样的计算相似度的办法以及更多的参数。
• 如果直接对原始的Embedding做自注意力操作，则计算的相似度结果是个对称矩阵，对角线上的值一定是最大的。因为每个字词必定最关心自己，这样背离了自注意力操作的初衷。
• $Q * K^T$大概率会得到一个类似单位矩阵的attention矩阵，这样self-attention就退化成一个point-wise线性映射，捕捉注意力的能力就会受限，i，j位置之间的前后向注意力就会变得一样。而我们一般期望两个token在一句话中先后顺序也能反映一定的不同信息。对于两个词语，A对于B的重要性，不一定等同于B对A的重要性。比如：“A爱B”和“B爱A”的程度不一定一样。
• 这个对称矩阵的对角线上的值大概率是本行最大的，这样softmax后对角线上的注意力一定是本行最大，也就是不论任何位置任何搭配，每个token的注意力几乎全在自己身上，这样违背了Transformer用自注意力机制捕捉上下文信息的初衷。

我们再看看使用权重矩阵的优势所在。

• 匹配。$a_{ij}$要通过计算$h_i$和$h_j$之间的关系得到，一个最简单的办法是把这两个矩阵直接相乘。但是这样可能会有问题：两个矩阵可能形状不匹配，没法直接做矩阵乘法。而给这两个矩阵分别左乘一个矩阵$W^K$和$W^Q$就可以解决上述两个问题。
• 可学习。在注意力机制中，每一个单词的query, key,value应该不仅仅只和该单词本身有关，而应该是和对应任务相关。每个单词的query, key, value不应该是人工指定的，而应该是可学习的。因此，我们可以用可学习的参数来描述从词嵌入到query, key,value的变换过程。这样经过大量训练之后，每个元素都会找到完成各自任务所需的最合适的query, key,value。这些相关的训练参数就在三个权重矩阵中。
• 增加拟合能力。三个权重矩阵都是可训练的，这增加了模型可学习的参数量，扩展了特征空间，增加了模型的拟合能力。
• 信息交换。我们指定输入矩阵的第 i 行表示第 i 个时刻的输入 $x_i$。对于此矩阵中的向量来说，权重矩阵$W^T, W^Q, W^V$在整体运行过程中是共享的，即，不同的$x_i$共享了同一个$W^T, W^Q, W^V$，通过这个操作，$x_1$和$x_2$已经发生了某种程度上的信息交换。也就是说，单词和单词通过共享权重已经相互发生了一定程度的信息交换。

另外，也许读者会问，既然Q和K都是一样维度，为什么不合用一个权重矩阵呢？或者说，为何要使用三个不同的权重矩阵？使用不同的权重矩阵生成的主要原因是：为了提供更灵活的模型表示能力和捕捉数据中的复杂依赖关系。其实，此处也回答了为何要区分Q、K和V。

• 增加表达能力。加入了不同的线性变换相当于对 x 做了不同的投影，将向量 x 投影到不同空间，这意味着Q和K可以在不同的语义空间中进行表达，有助于模型捕捉更丰富的语义信息和依赖关系。
• 区分不同匹配或者说角色分离：在自注意力机制中，Q、K和V扮演着不同的角色。Q代表了我们要查询的信息或者说当前位置希望获得的信息，K代表了我们用来与Q匹配的键或者说序列中各位置能提供的信息，而V代表了一旦找到匹配者我们要提取的值或者说应该从各位置获取的实际内容。使用不同的权重矩阵能够更好地区分这些不同的角色，使用不同的权重矩阵为Q和K提供了能力去捕捉不同的依赖关系，增强了模型对输入数据的理解，提高模型的效果。
• 增加灵活性。如果 Q 和 K 使用相同的权重矩阵，则其结果和使用 X 自身进行点乘的结果相同，那么它们之间的关系会被严格限制在一个固定的模式中，这限制了模型的灵活性。而直接从 Q 得到 V 会忽略了通过 K 来确定相关性的重要性，也减少了模型处理信息的灵活性。
• 并行处理。Transformer模型的设计允许在处理序列时进行高效的并行计算。Q、K、V的独立使得模型可以同时计算整个序列中所有位置的注意力分数，这大大提高了计算效率。

总的来说，虽然在某些情况下使用相同的键进行自身的点乘（或者共享权重矩阵）可能也能工作得很好，但使用不同的权重矩阵为Q和K提供了更大的灵活性和表示能力，有助于提升模型性能和泛化能力。

我们再用三个权重矩阵来细化注意力公式如下。

2.2 计算过程

缩放点积注意力（Scaled Dot-Product Attention）模块的公式如下：

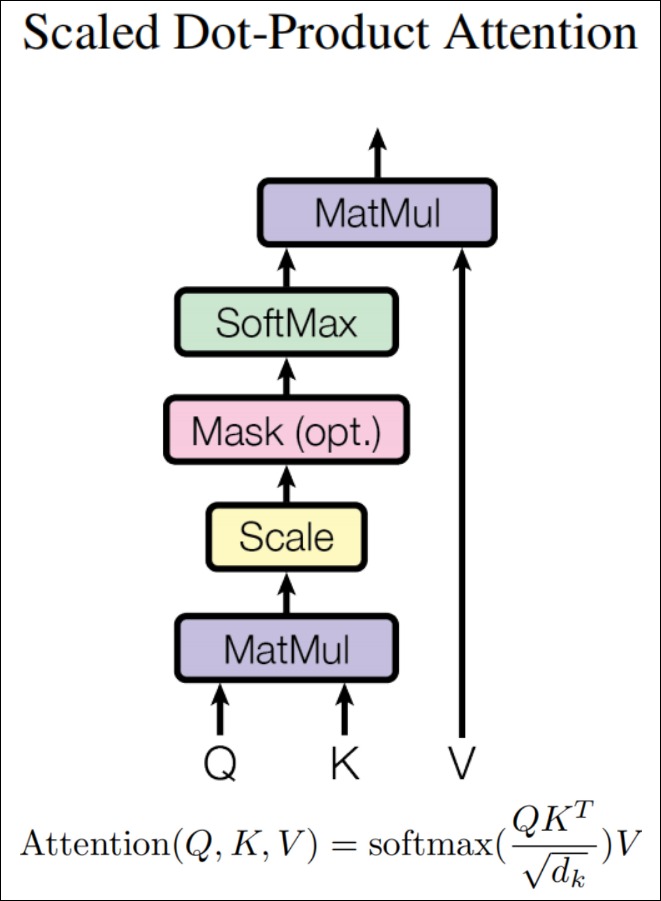
此公式中, $d_k$ 是向量的维度, 且 $d_k = d_q = d_v$, 如果只设置了一个头, $d_k$ 就是模型的维度 $d_{model}$, 如果设置了8个头, 则 $d_k = d_{model}/8$, 且如果模型的维度是 512 维, 则 $\sqrt{d_k}$ 即等于8。Q 和 K 的维度均是 $(L, d_k)$, V 的维度是 $(L, d_v)$, 其中 L 是输入序列长度。$softmax(QK^T)$ 的维度是 $(L, L)$, $Attention(Q,K,V)$ 的输出维度是 $(L, d_v)$。

我们梳理下计算过程如下（对应上图中从下到上的顺序）:

• 输入。Q、K、V是把输入映射成高维空间的点, 它们之间的关系通过后续的变换来捕捉。
• 计算分数（score function）。Query和所有的Key进行相似度计算, 得到注意力分数（查询的相关性）。计算公式为$s_i = a(q_i, k_j)$。也就是Q矩阵和K矩阵的转置之间做矩阵乘法（即点积）。这一步是计算在高维空间中度量向量之间的相似性。
• 缩放。对得分矩阵scores进行缩放, 即将其除以向量维度的平方根$\sqrt{d_k}$。
• 掩码。若存在掩码矩阵, 则将掩码矩阵中值为True的位置对应的得分矩阵元素置为负无穷。这是由于在整个模型的运行过程中, 可能需要根据实际情况来忽略掉一些输入。我们将在下一篇进行详细解释。
• 归一化（alignment function）。对点积结果进行归一化, 即使用softmax操作将权重进行归一化, 这样可以更加突出重要的权重。计算公式为$a = softmax(s)$。这一步是将实数域的分数映射到概率分布上。
• 生成结果（context vector function）。使用a对Value进行加权平均的线性变换, 可以理解为输出是在value之间根据key-query的相似度进行内插值。计算公式为$Attention Value = \sum_i a_i v_i$。

从泛函分析的角度来看, Attention机制中的相关性计算和加权求和步骤可以看作是对输入向量空间的一种动态变换。这种变换不是固定的, 而是依赖于输入数据的内容来决定的。

我们接下来对上面过程中的一些重点进行详细梳理。

2.3 点积注意力函数

Transformer论文使用了乘法函数或者说点积注意力函数来计算相似度。从抽象代数的角度来看, 注意力机制更像是一个关系运算: 用两个元素之间的关系（比如相似度）来决定两个元素是否属于同一个类。分类之后才会基于输入元素之间的相似性进行加权组合。

方案选择

如下所示, 常见的相似度计算有点积（相乘）和相加。

$$

\begin{align*}

sim(q,k) &= q^T k \quad [内积相似度] \

sim(q,k) &= w^T [q;k] \quad [拼接相似度] \

sim(q,k) &= \frac{q^T k}{||q||\cdot||k||} \quad [余弦相似度]

\end{align*}

$$

其中拼接相似度是将两个向量拼接起来, 然后利用一个可以学习的权重$w$来内积得到相似度, 也称为Additive Attention, 意思是指$w^T [q;k] = w_q^T q + w_k^T k$。

对应到V则是:

$$

\begin{align*}

attention(q,k,v) &= W_c \cdot tanh(W_k k + W_q q) \quad [相加] \

attention(q,k,v) &= W_c \frac{(W_k k)(W_q q^T)}{\sqrt{d}} \quad [相乘]

\end{align*}

$$

从公式中可以看到, 加法方案优点是:

• 可以处理不同维度的 key 与 query（而点积操作要求 query 和 key 具有相同的长度）。
• 计算更简单，但是外面套了tanh和v，相当于一个完整的隐层，因此整体复杂度其实和乘法方案接近。
• 虽然在大多数任务中，点乘注意力和加法注意力的性能差异不大，但是在某些长序列任务中，加法注意力可能会略优于点乘注意力。

而且，乘法方案还有一个劣势是：随着向量维度的增大，点乘结果的上限越来越高，点乘结果的差异越来越大，因此计算Attention权重需要加入scaled。

从表现效果来讲，论文”Massive Exploration of Neural Machine Translation Architectures“对此做了对比实验。

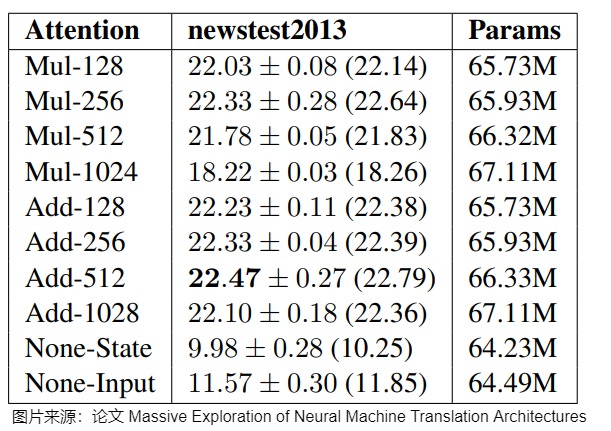
从结果上可以看得出，加法式注意机制略微但始终优于乘法式注意力机制。

那么为何Transformer为何选取点积注意力而非用加法注意力？网络上也有一些讨论，给出的一些思考点是：

• 点乘操作可以通过矩阵乘法高效地在硬件上并行化，从而实现快速计算。
• 点乘注意力能够捕捉查询和键之间的相似度，当查询和键相似时给予更高的权重，这有助于模型捕捉输入序列中的复杂依赖关系。
• 在将表示分割成不同个头进行运算时，使用点乘会更加灵活方便计算。

论文中给出的原因是基于效率和建模能力的考虑，具体如下：

我们再来看看苏剑林大神对公式的精彩解读，借此可以对公式有更加深刻的理解。

将$QK^T$进行拆解，得到两个向量的乘积为：$q_i \cdot k_j = | q_i | | k_j | \cos(q_i, k_j)$，即将两个向量的乘积分解为了两个向量各自模长与夹角余弦的乘积。其中：

• $| q_i |$只跟当前位置有关，因此它不改变注意力的相对大小，而只改变稀疏程度。
• $| k_j |$是其它位置的的张量模长，有能力改变条件概率$p(j|i)$的相对大小，但它不涉及到$i,j$的交互，只能用来表达一些绝对信号。
• $\cos(q_i, k_j)$就是用来表达$i,j$的交互，是自由度最大的一项。

为了提高某个位置的相对重要性，模型有两个选择：

• 增大模长$| k_j |$。
• 增大$\cos(q_i, k_j)$，即缩小$q_i, k_j$的夹角大小。

然而，由于“维度灾难”的存在，在高维空间中显著地改变夹角大小相对来说没有那么容易，所以如果能靠增大模长$| k_j |$完成的，模型会优先选择通过增大模长$| k_j |$来完成，这导致的直接后果是：$\cos(q_i, k_j)$的训练可能并不充分（指被训练过的夹角只是一个有限的集合，而进行长度外推时，它要面对一个更大的集合，从而无法进行正确的预测），这可能是Attention无法长度外推的主要原因。

2.4 softmax

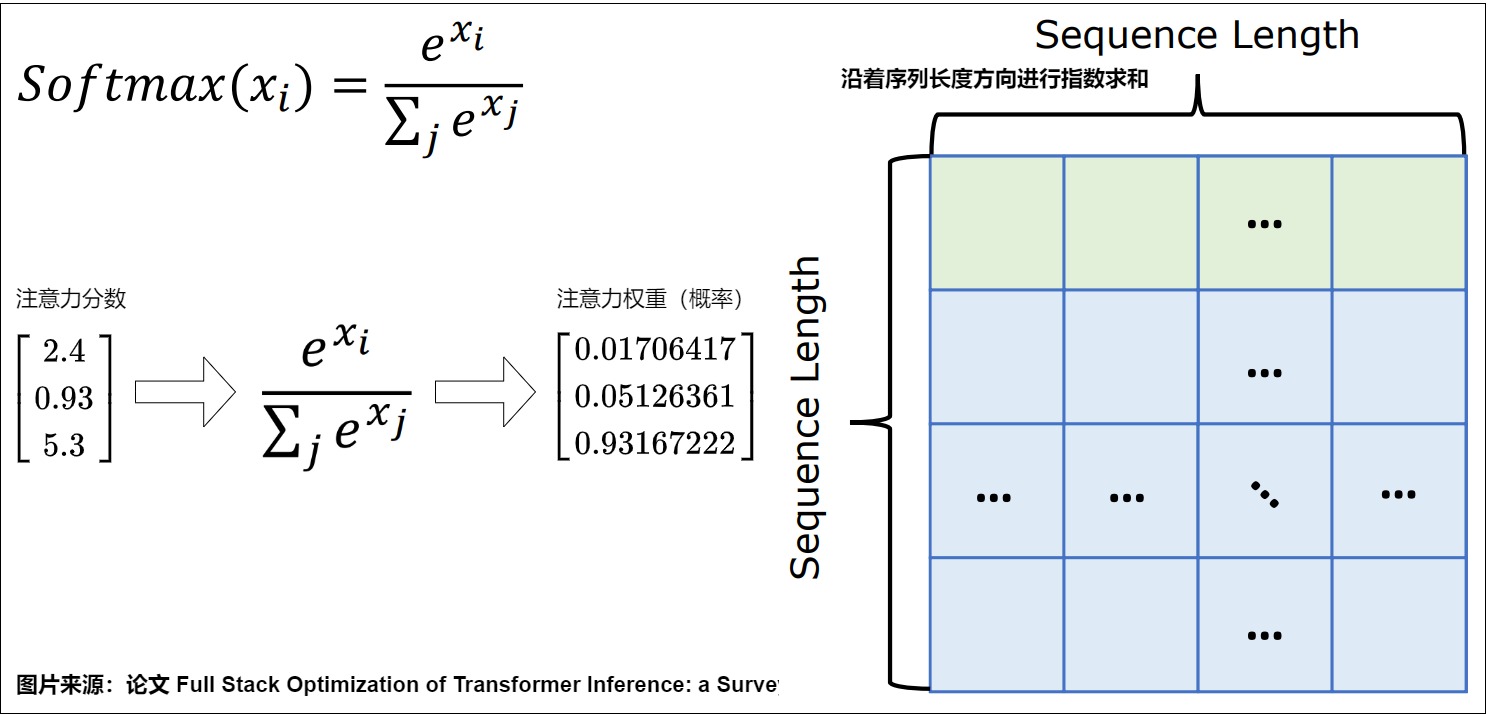
定义

Softmax操作的意义是归一化。我们将没有做softmax归一化之前的结果称为注意力分数，将注意力分数经过softmax归一化后的结果称为注意力权重。给定一个包含$n$个实数的向量$\boldsymbol{x} = [x_1, x_2, \dots, x_n]$，Softmax函数将其转换为一个概率分布$\boldsymbol{p} = [p_1, p_2, \dots, p_n]$，其中每个$p_i$的计算公式为：

$$

p_i = softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}

$$

Softmax关键性质如下：

1. 非负性：对于任意$i$，$p_i \geq 0$。
2. 归一化：所有输出的和为1，即$\sum_{i=1}^n p_i = 1$。
3. 指数函数的使用：指数函数$e^{x_i}$确保了输出值为正，并且放大了较大的$x_i$值的差异。

算法

算法流程需要两个循环，首先需要迭代计算分母的和，然后再迭代计算向量中每一个值对应的 softmax 值，即缩放每一个元素。这个过程需要两次从内存读取和一次写回内存操作。具体算法如下，其中 $d_v$ 就是分母。

具体图例如下。

必要性

softmax函数之所以在神经网络中得到广泛应用，是如下原因：

• softmax在推理时可以将输出层的原始输出（logits）转换为有效的概率分布，使得输出具有概率的物理意义，便于解释和计算损失函数，同时保持数值稳定性和对称性。这使得softmax成为多类分类问题中的首选激活函数。
• 在训练时指导模型学习。在神经网络的训练过程中，通常会使用交叉熵损失函数来配合softmax函数。交叉熵损失函数能够量化模型输出的概率分布与真实标签之间的差异，而softmax函数的输出提供了一个概率分布。这种机制使得模型能够在训练过程中更有效地调整权重，以提高对真实概率分布的估计准确性。

为何要在注意力机制中加入 softmax？因为看起来 softmax 是有害无益，比如：

• 如果没有 Softmax，则计算复杂度会大幅度降低。因为去除 softmax 之后，我们得到三个矩阵连乘 $QK^TV$，而矩阵乘法是满足结合率的，所以我们可以先算 $K^TV$，得到一个 $d×d$ 的矩阵，然后再用 Q 左乘它，由于 $d«n$，所以这样算大致的复杂度只是 $O(n)$。即，去掉 Softmax 的 Attention 的复杂度可以降到最理想的线性级别 $O(n)$。
• 如果没有Softmax，则内存占用会大幅度降低。这里我们提前看看FlashAttention所要解决的困境。如果没有softmax的话，我们可以对矩阵采用分块（Tiling）计算。比如，我们可以把Q, K, V沿着N（seqence length维度）切成块，算完一块Q和一块$K^T$之后，立刻和一块V进行矩阵矩阵乘法运算（GEMM）。一方面，避免在HBM和SRAM中移动P矩阵，另一方面，P矩阵也不需要被显式分配出来，消除了HBM中$O(N^2)$级别的存储开销。

在注意力机制中加入softmax是因为其有如下优点或者功能。

Softmax 操作实质上是在量化地衡量各个词的信息贡献度。因为在注意力机制中，我们在直觉上是希望关注语义上相关的单词，并弱化不相关的单词。这其实是一个多分类问题。在多分类问题中，我们希望神经网络的输出可以反映每个类别的概率，即每个输出节点的值代表了相应类别的概率。这要求输出值必须满足两个条件：

• 首先，每个输出值都应该在0到1之间；
• 其次，所有输出值的和应该等于1。 这样，输出就可以被解释为概率分布。直接的线性归一化虽然可以满足第一个条件，但往往不能满足第二个条件，因为它没有考虑分值间的相对差异，不能反映出原始分值中的相对强度或置信度。而 softmax 函数恰好能够同时满足这两个条件。

Softmax函数通过对每个分值应用指数函数，然后对这些指数值进行归一化处理来转换为概率，这样既保证了每个输出值在0到1之间，又保证了所有输出值之和为1。更重要的是，指数函数的使用放大了分值之间的差异，更好的反映了原始分值中的相对置信度。

在给定一组数组成的向量，Softmax先将这组数的差距拉大（由于exp函数），然后归一化，它实质做的是一个soft版本的argmax操作，或者当作argmax的一种平滑近似。与argmax操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。因此得到的向量接近一个one-hot向量（接近程度根据这组数的数量级有所不同）。

另外，KQ两个矩阵相乘，线性乘积下秩不会超过d，softmax后会有一定程度的增秩效果，如果不使用softmax，线性attention的秩更低，表达能力也更差。

缺点

Softmax 也存在一些固有限制。比如论文"softmax is not enough (for sharp out-of-distribution)“指出：softmax 函数在输入规模增大时，其输出系数会趋于均匀分布（注意力分散）。即，即便这些 token 的注意力系数在分布内是尖锐的（even if they were sharp for in-distribution instances），输入更多的 token 会导致注意力更加分散（或者说注意力的熵变大），从而导致训练和预测的结果不一致。具体如下图所示。

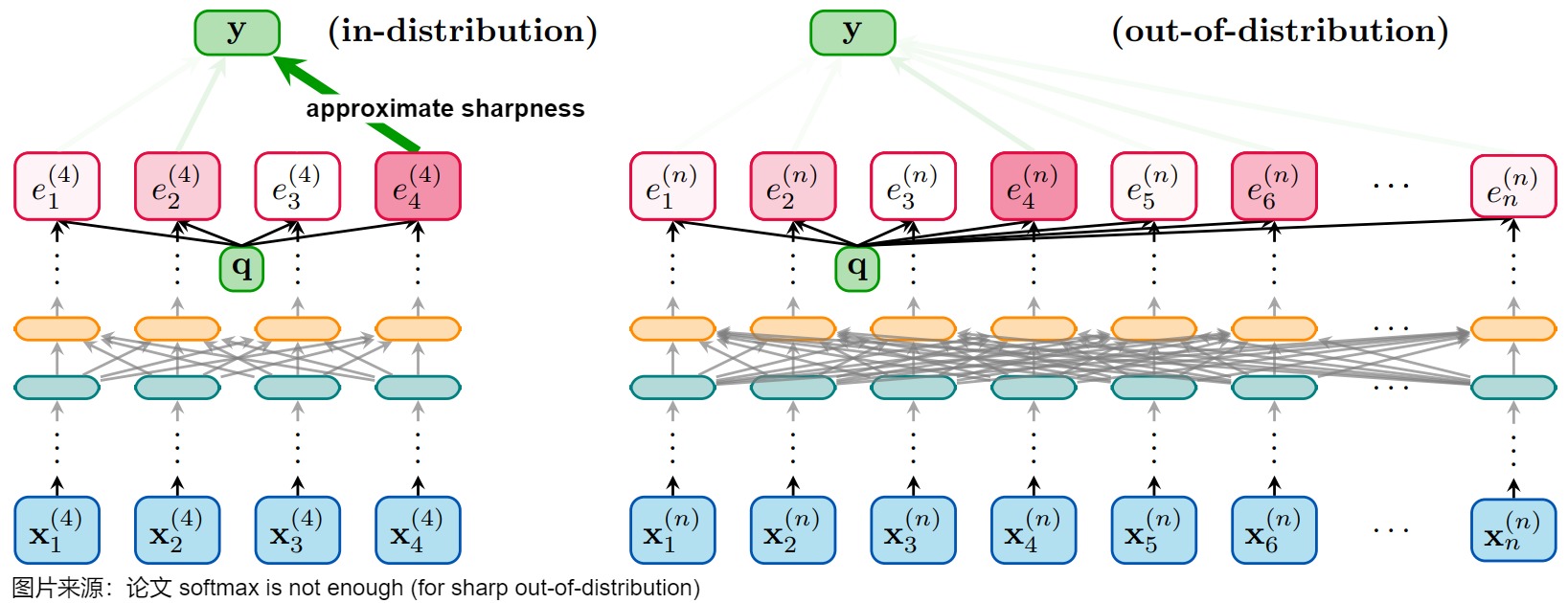
该论文提醒我们，即使是像softmax这样广泛使用的函数，也可能存在其适用范围的局限性，尤其是在处理超出训练分布的数据时。我们需要更加重视模型的泛化能力，并探索更鲁棒的模型架构。

改进

人们对 softmax 也有很多改进。

Log-Softmax

标准的softmax公式涉及到了很多的求幂和除法，导致计算成本较高，我们可以通过对数值取log，使得计算成本降低。具体如下：

$$

log\ softmax(x_i) = log\frac{e^{x_i - c}}{\sum_{j=1}^d e^{x_i - c}} = x_i - c - log\sum_{j=1}^d e^{x_i - c}

$$

这种方式叫作Log-Softmax。与Softmax 相比，使用 Log-Softmax 有许多优点，包括提高数值性能和梯度优化等。这些优势对于实现非常重要，尤其是当训练模型在计算上的成本很高时，其能带来很客观的收益。而且log 概率的使用，具有更好的信息理论可解释性，当用于分类器时，Log-Softmax 在模型无法预测正确的类别时会惩罚模型。

Hierarchical Softmax(H-Softmax)

标准softmax的时间复杂度都是 $O(n)$，这在分类任务中可能影响不大，只需要在最后的一层后面进行一次 $O(n)$ 计算就可以了。但是在NLP的生成任务中，我们需要对词表大小的向量进行Softmax，是为了把每个词的Softmax值用作似然，从而挑选出似然最大的那个词。一旦词表特别大，计算量将是一个严峻的问题，每次预测一个token都需要$O(|V|)$的时间复杂度。所以需要对Softmax进行一定的改造来适应实际任务，而H-Softmax就是用来解决这个问题的。

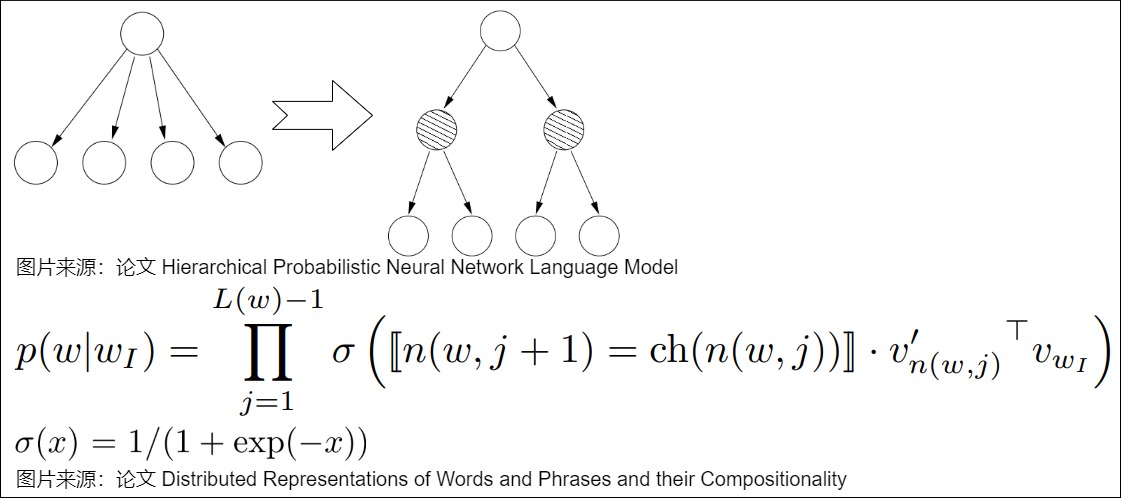
H-Softmax就是Word2vector中的Hierarchical Softmax。H-Softmax的解决方案是将Huffman Tree融入进来，将原先用 softmax 做多分类分解成多个sigmoid，然后使用Logistic Regression判断在哈夫曼树中走左子树还是右子树，最后其输出的值就是走某一条树分支的概率。

分层 softmax 使用输出层的二叉树表示，假设 $W$ 个词分别作为叶子节点，每个节点都表示其子节点的相对概率。词表中的每个词都有一条从二叉树根部到自身的路径。用 $n(w,j)$ 来表示从根节点到 $w$ 词这条路径上的第 $j$ 个节点，用 $ch(n)$ 来表示 $n$ 的任意一个子节点，设如果 $x$ 为真则 $[x]=1$，否则 $[x]=-1$，那么 Hierarchical Softmax 可以表示为下图。

adaptive softmax

常见的对softmax改进方法可以大致区分为两类：一是准确的模型产生近似概率分布，二是用近似模型产生准确的概率分布，这些都是从数理角度进行优化。但是从硬件的角度，应该如何配合GPU进行优化呢？

论文“Efficient softmax approximation for GPUs"提出的Adaptive Softmax就给出了一些思路。Adaptive Softmax借鉴的是Hierarchical Softmax和一些变型，与以往工作的不同在于，该方法结合了GPU的特点进行了计算加速，这样可以提高softmax函数的运算效率，适用于一些具有非常大词汇量的神经网络。

想法很简单，文章的大多数词都由词汇表里的少数词构成，即长尾理论或28原则。而语言模型在预测词的时候往往需要预测每个词的概率（通常是softmax），词汇表可能非常大，低频词非常多。那么就可以利用单词分布不均衡的特点，在训练时把词语分成高频词和低频次两类，先预测词属于哪一类，然后再预测具体是哪个词，这样简单的分类就使得softmax的计算量大大减少。原来是每个词都要计算一次， 现在是：V(高频) + P(低频) * V(低频)，V(高频) 会大幅变小，V(低频)虽然大但是P(低频) 很小。另外，Adaptive Softmax也通过结合现代架构和矩阵乘积操作的特点，通过使其更适合GPU单元的方式进一步加速计算。

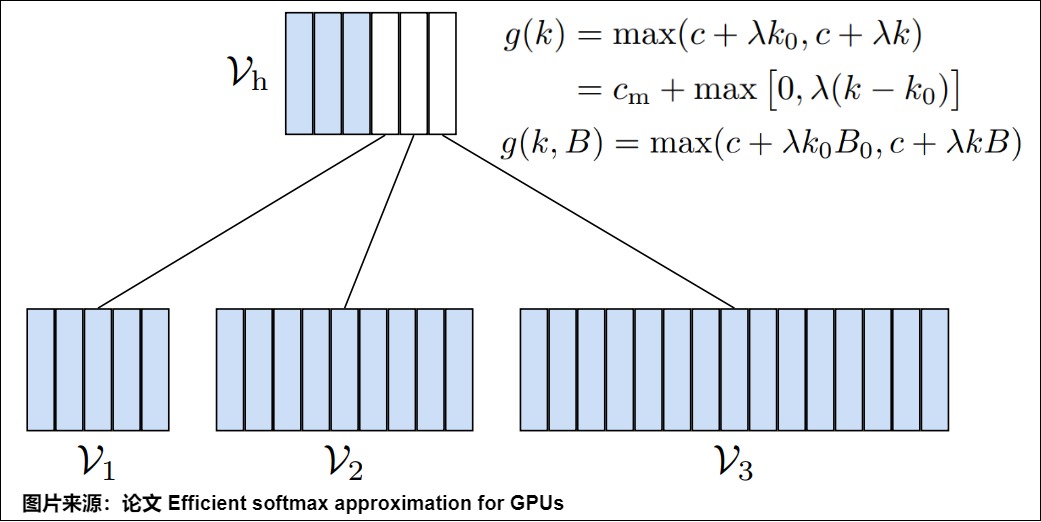
Adaptive Softmax 的层次模型被组织为

• 第一层，包括最频繁的单词和表示聚类的向量.
• 第二层上是与罕见单词相关的聚类，最大的聚类的与最不频繁的单词相关。具体如下图所示，蓝色表示高频词（总体分作一类），白色是表示低频词（这里有三个白色框，就代表三类低频词），每个 time step 中，先预测当前词是哪一类（高频词还是低频词分类），然后再在所得的分类中进行 Softmax 计算，从而得到最终的结果。

那么如何进行分类呢？论文也给了一个计算的模型，假设 B 是 batch size，d 是 hidden layer 的 size，k 是 feature 的大小，具体见下图上的公式。

2.5 缩放

缩放点积注意力（Scaled Dot-Product Attention）中的Scaled是缩放的意思，是在点乘之后除以一个分母。因此我们提出了一个问题，注意力的计算公式中 $\text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right)$ 为什么要除以 $\sqrt{d}$？

结论

我们细化原始论文的解释如下： 当维度$d_k$较大时，$q$和$k$的的点积会容易出现较大数值（正比于维度），当这些大数值经过softmax函数时，点积结果的分布会趋近于陡峭（分布的方差大，分布集中在绝对值大的区域）。进而会把点积结果推向softmax函数的梯度平缓区，导致 softmax 函数的梯度将变得非常小，这意味着模型将难以收敛，加大学习难度。因此Transformer作者将乘法函数按照因子$1/\sqrt{d_k}$进行缩放，这样$\text{softmax}(QK^T)$分布的陡峭程度就和$d_k$解耦了。正好抵消了维度增加造成的点积尺度放大效应，可以保证无论维度$d_k$取什么值，点乘的结果都处在一个合理的范围内，从而有助于保持梯度的稳定性，加速模型的训练过程。

对于较大数值这部分，可以参见论文脚注。

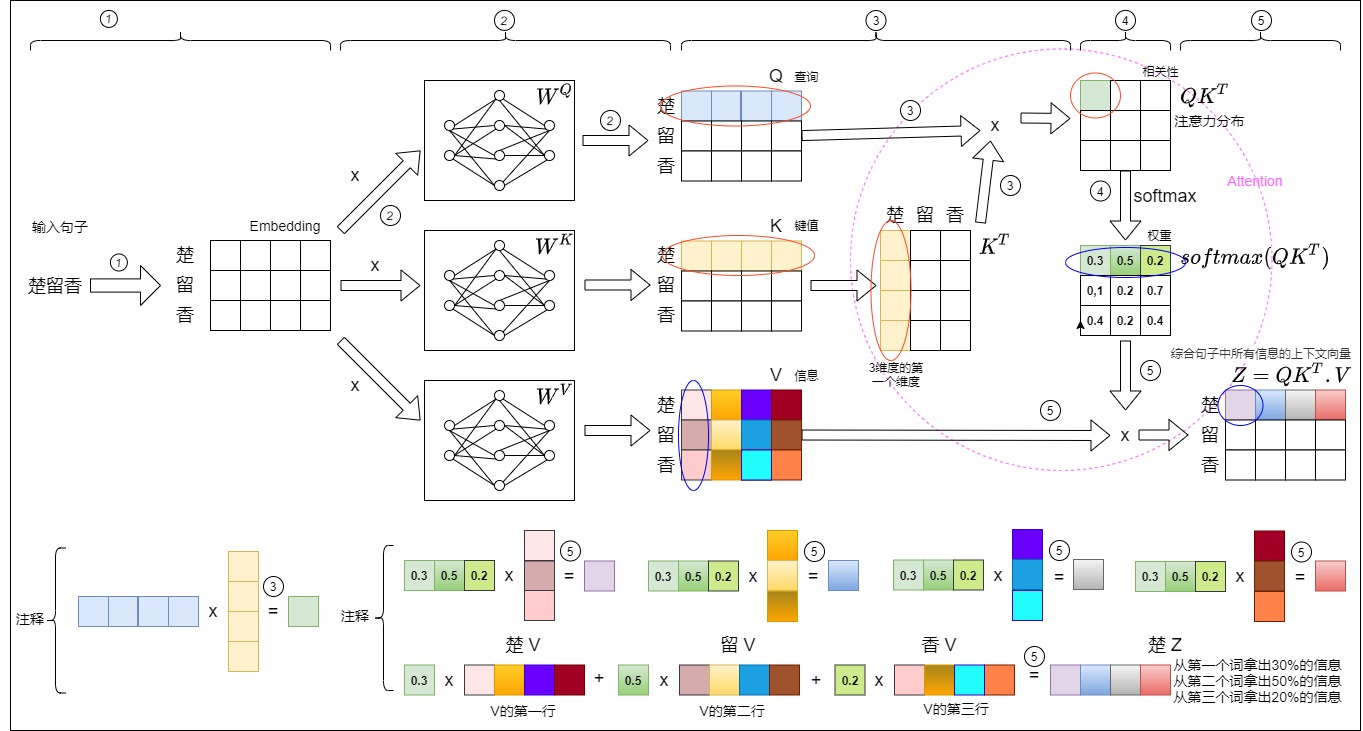
最后，我们梳理自注意力机制的计算过程如下图所示。

参考资料

• https://www.cnblogs.com/rossiXYZ/p/18751758