动态连通性

有 N 个对象，对象之间可以连通。那么这 N 个对象就可能形成 M 个集合。

我们继续假设： “相连（is connected to）” 是两个数之间的一种关系，且这种关系满足以下条件：

  • 自反性（Reflexive）： p 和 p 是相连的；

  • 对称性（Symmetric）： 如果 p 和 q 是相连的，那么 q 和 p 也是相连的；

  • 传递性（Transitive）： 如果 p 和 q 相连且 q 和 r 相连，那么 p 和 r 相连。

    当两个数相连时，它们属于同一个 等价类（Connected Components）。 等价类，就是所有相连的数的集合，这个集合必须包含所有相连的数。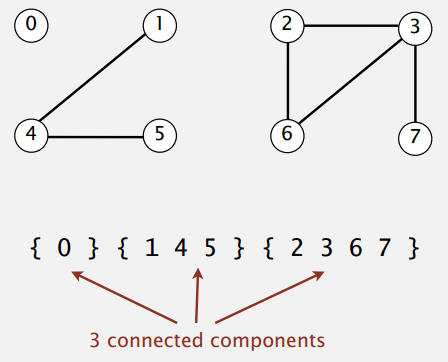

    ConnectedComponents
    ConnectedComponents

对于这些对象，有两个操作

  • Union(x, y)可以连接两者
  • Find(x)来查询对象 x 属于哪个集合

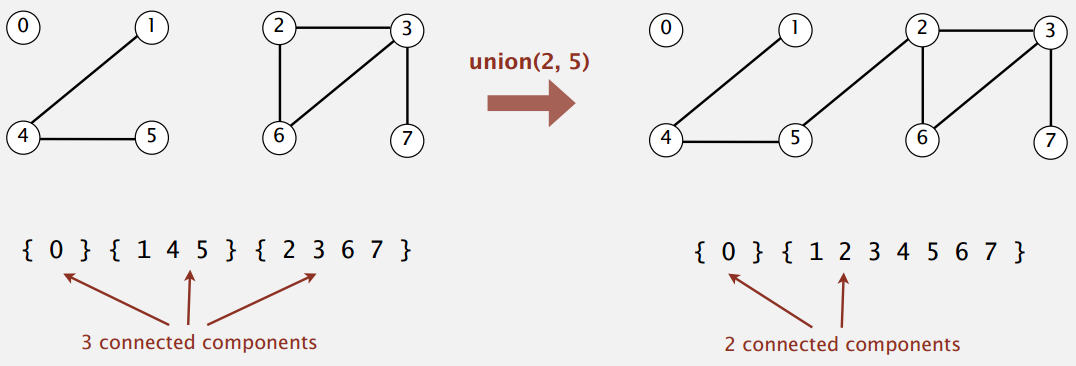
UnionFindOperation
UnionFindOperation
并查集(UnionFind)是解决动态连通性最常用的一个数据结构

并查集

Quick Find 算法

  • 整数型数组 id[]，长度为 N。
  • p 和 q 是相连的等价于数组中 p 下标和 q 下标的数相同。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include <vector>
using namespace std;

class DisjointSet {
private:
	vector<int> parent;
public:
	DisjointSet(int maxSize) : parent(vector<int>(maxSize)) {
		// 初始化每个元素的根节点都为自身
		for (int i = 0; i < maxSize; ++i)
			parent[i] = i;
	}

	void Union(int x, int y) {
		int xParent = parent[x];
		int yParent = parent[y];
		if (xParent == yParent) return;

		for (int i = 0; i < parent.size(); i++) {
			if (parent[i] == xParent)
				parent[i] = yParent;
		}
	}

	int Find(int x) {
		return parent[x];
	}

	bool Connected(int x, int y) {
		return parent[x] == parent[y];
	}
}

算法分析

QuickFind 算法太慢了。 下表是最坏情况下 QuickFind 算法对一组点操作使用的时间消耗。

算法 初始化 union 操作 find 操作
QuickFind N N 1

Union 操作过于缓慢：如果要对 N 对点进行 union 操作，最多需要对数组访问 N^2 次。

Quick Union 算法

  • 整数型数组 id[]，长度为 N。
  • id[i]中存储 i 的父节点（ 也就是形成一个链接，直到其父节点就是它自己，说明到头了）
  • i 的根节点（root）是 id[id[id[id[…id[i]…]]]]
    QuickUnion
    QuickUnion
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#include <vector>
using namespace std;

class DisjointSet {
private:
	vector<int> parent;
public:
	DisjointSet(int maxSize) : parent(vector<int>(maxSize)) {
		// 初始化每个元素的根节点都为自身
		for (int i = 0; i < maxSize; ++i)
			parent[i] = i;
	}

	void Union(int x, int y) {
		int i = Find(x);
		int j = Find(y);
		parent[i] = j;
	}

	int Find(int x) {
		return parent[x] == x ? x : Find(parent[x]);
	}

	bool Connected(int x, int y) {
		return Find(x) == Find(y);
	}
}

算法分析

对一对点进行操作需要访问数组的次数，图中是最坏情况。

算法 初始化 union 操作 find 操作
QuickFind N N 1
QuickUnion N N* 1

*：包括了寻找根节点的操作。

QuickFind 的缺点

  • Union 操作太慢了，最差为 N
  • 树是平的，但是维护这个状态时间耗费太大了

QuickUnion 的缺点

  • 树可能会很高
  • Find 操作太慢了，最差为 N

算法优化

加权 Weighting

加权 QuickUnion（Weighted QuickUnion）

  • 改进 QuickUnion，避免太高的树
  • 对每个树的大小（包含点的数量）进行记录
  • union 操作时，比较两个点所在树的大小，小数的根节点连接到大树的根节点之上

数据结构其实和 QuickUnion 相同，但是需要再维护一个额外的数组 sz[i]，用来记录以 i 节点为根节点的分量的大小（及分量中数的多少）

路径压缩 Path Compressing

在计算点 p 的根节点 root 之后，每个经过的节点，如果其根节点不为 root 的话，让其根节点变成 root，如图是带路径压缩的 QuickUnion 算法（Quick Union with Path Compression），下图是具体的过程。

优化后的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include <vector>
using namespace std;

class DisjointSet {
private:
	vector<int> parent;
	vector<int> rank;
public:
	DisjointSet(int maxSize) : parent(vector<int>(maxSize)),
							   rank(vector<int>(maxSize, 0))
	{
		// 初始化每个元素的根节点都为自身
		for (int i = 0; i < maxSize; ++i)
			parent[i] = i;
	}

	void Union(int x, int y) {
		int i = Find(x);
		int j = Find(y);

		if (rank[i] > rank[j]) parent[j] = i;
		else {
			parent[i] = j;
			if (rank[i] == rank[j]) ++rank[j];
		}
	}

	int Find(int x) {
		return parent[x] == x ? x : (parent[x] = Find(parent[x]));
	}

	bool Connected(int x, int y) {
		return Find(x) == Find(y);
	}
}

算法分析

使用带路径压缩的加权 Quick Union 算法，对于 N 个数，M 次操作时，访问数组次数最多为 c (N + M lg* N)。 （c 为常数， lg* N 是 lg(lg(lg(…lg()…)))。）

对于 N 个数，M 次操作时，有没有线性访问数组次数的算法呢？

  • 理论上， WQUPC（Weighted Quick Union & Path Compression）不是线性的
  • 实际中，WQUPC 基本是线性的

现已证明，没有完全的线性算法存在的

参考资料

原理解析

动态连通性

有N个对象，对象之间可以连通。那么这N个对象就可能形成M个集合。

我们继续假设： “相连（is connected to）” 是两个数之间的一种关系，且这种关系满足以下条件：

  • 自反性（Reflexive）： p和p是相连的；

  • 对称性（Symmetric）： 如果p和q是相连的，那么q和p也是相连的；

  • 传递性（Transitive）： 如果p和q相连且q和r相连，那么p和r相连。

    当两个数相连时，它们属于同一个等价类（Connected Components）。 等价类，就是所有相连的数的集合，这个集合必须包含所有相连的数。

    ConnectedComponents
    ConnectedComponents

对于这些对象，有两个操作

  • Union(x, y)可以连接两者
  • Find(x)来查询对象x属于哪个集合

UnionFindOperation
UnionFindOperation
并查集(UnionFind)是解决动态连通性最常用的一个数据结构

并查集

Quick Find算法

  • 整数型数组id[]，长度为N。
  • p和q是相连的等价于数组中p下标和q下标的数相同。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include <vector>
using namespace std;

class DisjointSet {
private:
	vector<int> parent;
public:
	DisjointSet(int maxSize) : parent(vector<int>(maxSize)) {
		// 初始化每个元素的根节点都为自身
		for (int i = 0; i < maxSize; ++i)
			parent[i] = i;
	}

	void Union(int x, int y) {
		int xParent = parent[x];
		int yParent = parent[y];
		if (xParent == yParent) return;

		for (int i = 0; i < parent.size(); i++) {
			if (parent[i] == xParent)
				parent[i] = yParent;
		}
	}

	int Find(int x) {
		return parent[x];
	}

	bool Connected(int x, int y) {
		return parent[x] == parent[y];
	}
}
算法分析

QuickFind算法太慢了。 下表是最坏情况下QuickFind算法对一组点操作使用的时间消耗。

算法 初始化 union操作 find操作
QuickFind N N 1

Union操作过于缓慢：如果要对N对点进行union操作，最多需要对数组访问N^2次。

Quick Union算法

  • 整数型数组id[]，长度为N。
  • id[i]中存储i的父节点（ 也就是形成一个链接，直到其父节点就是它自己，说明到头了）
  • i的根节点（root）是id[id[id[id[…id[i]…]]]]
    QuickUnion
    QuickUnion
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#include <vector>
using namespace std;

class DisjointSet {
private:
	vector<int> parent;
public:
	DisjointSet(int maxSize) : parent(vector<int>(maxSize)) {
		// 初始化每个元素的根节点都为自身
		for (int i = 0; i < maxSize; ++i)
			parent[i] = i;
	}

	void Union(int x, int y) {
		int i = Find(x);
		int j = Find(y);
		parent[i] = j;
	}

	int Find(int x) {
		return parent[x] == x ? x : Find(parent[x]);
	}

	bool Connected(int x, int y) {
		return Find(x) == Find(y);
	}
}
算法分析

对一对点进行操作需要访问数组的次数，图中是最坏情况。

算法 初始化 union操作 find操作
QuickFind N N 1
QuickUnion N N* 1

*：包括了寻找根节点的操作。

QuickFind的缺点

  • Union操作太慢了，最差为N
  • 树是平的，但是维护这个状态时间耗费太大了

QuickUnion的缺点

  • 树可能会很高
  • Find操作太慢了，最差为N

算法优化

加权 Weighting

加权QuickUnion（Weighted QuickUnion）

  • 改进QuickUnion，避免太高的树
  • 对每个树的大小（包含点的数量）进行记录
  • union操作时，比较两个点所在树的大小，小数的根节点连接到大树的根节点之上

数据结构其实和QuickUnion相同，但是需要再维护一个额外的数组sz[i]，用来记录以i节点为根节点的分量的大小（及分量中数的多少）

路径压缩 Path Compressing

在计算点p的根节点root之后，每个经过的节点，如果其根节点不为root的话，让其根节点变成root，如图是带路径压缩的QuickUnion算法（Quick Union with Path Compression），下图是具体的过程。

优化后的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include <vector>
using namespace std;

class DisjointSet {
private:
	vector<int> parent;
	vector<int> rank;
public:
	DisjointSet(int maxSize) : parent(vector<int>(maxSize)),
							   rank(vector<int>(maxSize, 0))
	{
		// 初始化每个元素的根节点都为自身
		for (int i = 0; i < maxSize; ++i)
			parent[i] = i;
	}

	void Union(int x, int y) {
		int i = Find(x);
		int j = Find(y);

		if (rank[i] > rank[j]) parent[j] = i;
		else {
			parent[i] = j;
			if (rank[i] == rank[j]) ++rank[j];
		}
	}

	int Find(int x) {
		return parent[x] == x ? x : (parent[x] = Find(parent[x]));
	}

	bool Connected(int x, int y) {
		return Find(x) == Find(y);
	}
}

算法分析

使用带路径压缩的加权Quick Union算法，对于N个数，M次操作时，访问数组次数最多为c (N + M lg* N)。 （c为常数， lg* N是lg(lg(lg(…lg()…)))。）

对于N个数，M次操作时，有没有线性访问数组次数的算法呢？

  • 理论上， WQUPC（Weighted Quick Union & Path Compression）不是线性的
  • 实际中，WQUPC基本是线性的

现已证明，没有完全的线性算法存在的

具体题目

261 Graph Valid Tree

305 Number of Islands II

  • Islands are popping out of a grid sea. Give number of islands after each popping.
  • Maintain a parent set, do erase and insert during each union.

323 Number of Connected Components in an Undirected Graph

547 Friend Circles

721 Accounts Merge

785 Is Graph Bipartite?

  • For each node, merge all adjacent nodes. Then check for each edge.

803 Bricks Falling When Hit

  • Reverse-time union-find.

947 Most Stones Removed with Same Row or Column

  • Given stones on a 2D plane, one can remove a stone if there are other stones sharing the same row or column. Find maximum removes.
  • Union points by row or column.

952 Largest Component Size by Common Factor

  • Find the largest connected component of a graph, where there is an edge if two nodes share a common factor > 1.
  • O(N*sqrt(W)) time, where W is the maximum value in input array.

990 Satisfiability of Equality Equations

Reference