英文 缩写 中文释义
ViT Vision Transformers
CLIP Contrastive Language-Image Pre-training
DDPM1 Denoising Diffusion Probabilistic Models
DiT Diffusion Transformers
VAE Variational AutoEncoder
MAE Masked AutoEncoder
GAN Generative Adversarial Networks
U-Nets
BLIP Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation
CoCa Contrastive Captioners are Image-Text Foundation Models
LLaVA
GLIP
FID Frechet Inception Distance

前置数学知识

AutoEncoder

VAE

DDPM

DDPM1 的本质是通过模型学习训练数据的分布，产出尽可能符合训练数据分布的真实图片。

训练流程：

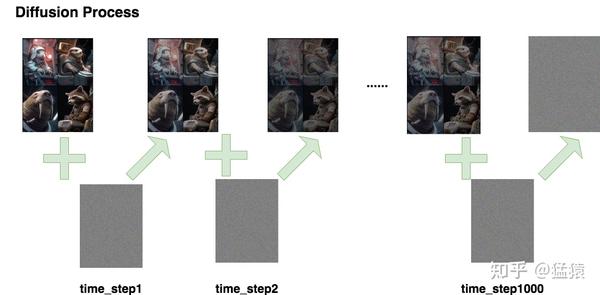
  • Diffusion Process，即 Forward Process，这个过程就是一步一步的去加噪声

  • Denoise Process，即 Reverse Process，这个过程是一步一步的去噪

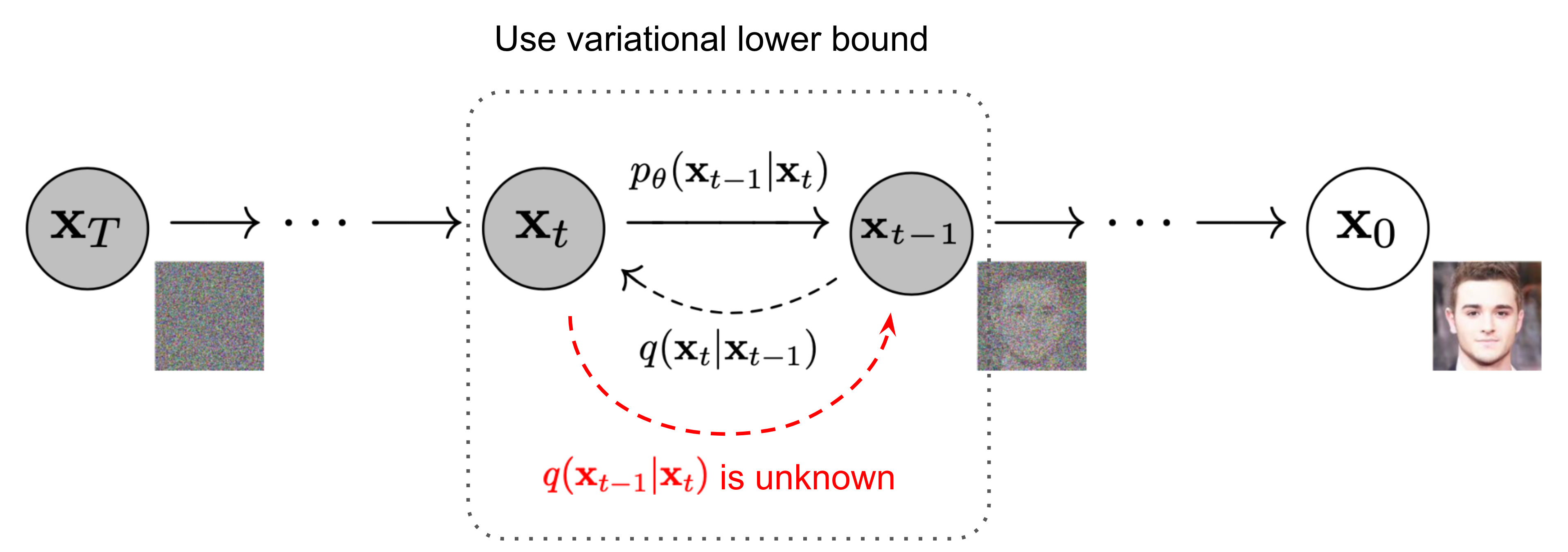
  • https://zhuanlan.zhihu.com/p/530602852

设置符号：

  • TT ：总步数
  • x0,x1,…,xT\mathbf{x}_0, \mathbf{x}_1, …, \mathbf{x}_T ：每一步产生的图片，其中 x0\mathbf{x}_0 是原始图片，xT\mathbf{x}_T 为纯高斯噪声
  • ϵ∼N(0,,1)\epsilon \sim \mathcal{N}(0,,1) ：为每一步添加的高斯噪声
  • $q(\mathbf{x}t \mid \mathbf{x}{t-1})： ： \mathbf{x}t在条件 在条件 \mathbf{x} = \mathbf{x}{t-1}$ 下的概率分布

Forward Diffusion Process

给定初始数据分布 x0∼q(x)\mathbf{x}_0 \sim q (\mathbf{x}) ，我们定义一个前向扩散过程 forward diffusion process：

  • 我们向数据分布中逐步添加高斯噪声，加噪过程持续 TT 次，产生一系列带噪声图片 x0,x1,…,xT\mathbf{x}_0, \mathbf{x}_1, …, \mathbf{x}_T
  • 在由 x𝑡−1\mathbf{x}_{𝑡−1}  加噪到 $\mathbf{x}𝑡 的过程中，噪声的标准差/方差是以一个在区间   的过程中，噪声的标准差/方差是以一个在区间 (0,1) 内的固定值  内的固定值 \beta_t 来确定的，均值是以固定值  来确定的，均值是以固定值 \beta_t 和当前时刻的图片数据   和当前时刻的图片数据 \mathbf{x}{t-1}$ 来确定的。

因此，根据以上流程

$$ \mathbf{x}t = \mathbf{x}{t-1} + \epsilon_{t-1} = \mathbf{x}_0 + \epsilon_0 + \epsilon_1 + … + \epsilon $$

对于最后一步： $$ \mathbf{x}T = \mathbf{x}{T-1} + \epsilon_{T-1} = \mathbf{x}0 + \epsilon_0 + \epsilon_1 + … + \epsilon{T-1} $$

其中：

$$ q (\mathbf{x}t \mid \mathbf{x}{t-1}) = \mathcal{N}(\mathbf{x}t; \sqrt{1-\beta_t} \mathbf{x}{t-1}, \beta_t \mathbf{I}) $$

$$ q(\mathbf{x}_{1:T} \mid \mathbf{x}0) = \prod{t=1}^T q (\mathbf{x}t \mid \mathbf{x}{t-1}) $$

上式意思是：

  • 由​ x𝑡−1\mathbf{x}_{𝑡−1}  得到​ ​ x𝑡\mathbf{x}_𝑡  的过程 ​ $𝑞(\mathbf{x}t|\mathbf{x}{t−1}) ，满足分布​  ，满足分布​  \mathcal{N}(\mathbf{x}t; \sqrt{1-\beta_t} \mathbf{x}{t-1}, \beta_t \mathbf{I})$
  • 这个分布是指以​ 1−βt\sqrt{1-\beta_t} 为均值，​βt​\beta_t 为方差的高斯分布
  • 我们看到这个噪声只由​ βt\beta_t 和 ​ x𝑡−1\mathbf{x}_{𝑡−1} 来确定，是一个固定值而不是一个可学习过程
  • 因此，只要我们有了​ x0\mathbf{x}_0 ，并且提前确定每一步的固定值，β1,β2,…,βT\beta_1, \beta_2, …, \beta_T ​，我们就可以推出任意一步的加噪数据 x1,…,xT\mathbf{x}_1, …, \mathbf{x}_T ​
  • 这里 Forward 加噪过程是一个马尔科夫链过程

随着​ tt 的不断增大，最终原始数据​ x0\mathbf{x}_0 会逐步失去它的特征。最终当 T→∞T \to \infty ​时， xT\mathbf{x}_T ​趋近于一个各向独立的高斯分布。从视觉上来看，就是将原本一张完好的照片加噪很多步后，图片几乎变成了一张完全是噪声的图片。

重参数

在逐步加噪的过程中，我们其实并不需要一步一步地从 x0,x1,…\mathbf{x}_0, \mathbf{x}_1,… 去迭代得到 xt\mathbf{x}_t 。事实上，我们可以直接从 $\mathbf{x}0和固定值序列 和固定值序列 {{\beta_T \in (0, 1)}}{t=1}^T$ 直接计算得到。

根据重参数技巧，我们可以一步推理出 xt\mathbf{x}_t，计算方法如下所示：

xt=αtˉx0+1−αtˉϵ \mathbf{x}_t = \sqrt{\bar{\alpha_t}} \mathbf{x}_0 + \sqrt{1-\bar{\alpha_t}} \epsilon

推导过程为：

设置 αt=1−βt\alpha_t = 1 - \beta_t， $\overline{\alpha}t = \prod{i = 1}^{T}\alpha_i，根据由​ ，根据由​ \mathbf{x}{𝑡−1} 得到​ ​   得到​ ​ \mathbf{x}𝑡 的过程​   的过程 ​ 𝑞(\mathbf{x}t|\mathbf{x}{t−1}) ，满足分布​  ，满足分布​  \mathcal{N}(\mathbf{x}t; \sqrt{1-\beta_t} \mathbf{x}{t-1}, \beta_t \mathbf{I})，有，有 $ \mathbf{x}t = \sqrt{1-\beta_t} \mathbf{x}{t-1} + \beta_t \epsilon{t-1} $$ 其中 $\epsilon{t-1}, \epsilon_{t-2},… \sim \mathcal{N}(0,,1)$ 为每一步添加的高斯噪声

$$ \mathbf{x}t = \alpha_t \mathbf{x}{t - 1} + (1 - \alpha_t) z_{t - 1}; \text{x}t{ where } z_{t - 1}, z_{t - 2}, \cdots \sim N(0, I) = \alpha_t \alpha_{t - 1} \mathbf{x}{t - 2} + (1 - \alpha_t \alpha{t - 1}) \overline{z}_{t-1} $$

  • ϵ∼N(μ,,σ2)\epsilon \sim \mathcal{N}(\mu,,\sigma^{2})

DDIM

Stable Diffusion

  1. Denoising Diffusion Probabilistic Models, Jonathan Ho, https://ar\mathbf{x}iv.org/pdf/2006.11239 ↩︎ ↩︎